An Data-Theoretic Account of Safe Brainwallets

An vital and controversial matter within the space of private pockets safety is the idea of “brainwallets” – storing funds utilizing a personal key generated from a password memorized fully in a single’s head. Theoretically, brainwallets have the potential to offer nearly utopian assure of safety for long-term financial savings: for so long as they’re saved unused, they don’t seem to be weak to bodily theft or hacks of any variety, and there’s no strategy to even show that you just nonetheless keep in mind the pockets; they’re as secure as your very personal human thoughts. On the similar time, nonetheless, many have argued towards the usage of brainwallets, claiming that the human thoughts is fragile and never nicely designed for producing, or remembering, lengthy and fragile cryptographic secrets and techniques, and so they’re too harmful to work in actuality. Which aspect is correct? Is our reminiscence sufficiently strong to guard our non-public keys, is it too weak, or is probably a 3rd and extra attention-grabbing risk really the case: that all of it is determined by how the brainwallets are produced?

Entropy

If the problem at hand is to create a brainwallet that’s concurrently memorable and safe, then there are two variables that we have to fear about: how a lot data we have now to recollect, and the way lengthy the password takes for an attacker to crack. Because it seems, the problem in the issue lies in the truth that the 2 variables are very extremely correlated; actually, absent a couple of sure particular sorts of particular tips and assuming an attacker working an optimum algorithm, they’re exactly equal (or slightly, one is exactly exponential within the different). Nonetheless, to begin off we will deal with the 2 sides of the issue individually.

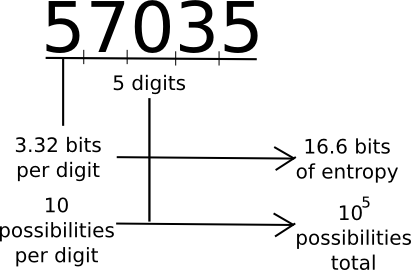
A typical measure that laptop scientists, cryptogaphers and mathematicians use to measure “how a lot data” a chunk of information comprises is “entropy”. Loosely outlined, entropy is outlined because the logarithm of the variety of attainable messages which are of the identical “type” as a given message. For instance, take into account the quantity 57035. 57035 appears to be within the class of five-digit numbers, of which there are 100000. Therefore, the quantity comprises about 16.6 bits of entropy, as 2^16.6 ~= 100000. The quantity 61724671282457125412459172541251277 is 35 digits lengthy, and log(10³⁵) ~= 116.3, so it has 116.3 bits of entropy. A random string of ones and zeroes n bits lengthy will include precisely n bits of entropy. Thus, longer strings have extra entropy, and strings which have extra symbols to select from have extra entropy.

Then again, the quantity 11111111111111111111111111234567890 has a lot lower than 116.3 bits of entropy; though it has 35 digits, the quantity will not be of the class of 35-digit numbers, it’s within the class of 35-digit numbers with a really excessive degree of construction; an entire listing of numbers with at the very least that degree of construction is likely to be at most a couple of billion entries lengthy, giving it maybe solely 30 bits of entropy.

Data concept has quite a few extra formal definitions that attempt to grasp this intuitive idea. A very widespread one is the thought of Kolmogorov complexity; the Kolmogorov complexity of a string is principally the size of the shortest laptop program that may print that worth. In Python, the above string can also be expressible as ‘1’*26+’234567890′ – an 18-character string, whereas 61724671282457125412459172541251277 takes 37 characters (the precise digits plus quotes). This offers us a extra formal understanding of the thought of “class of strings with excessive construction” – these strings are merely the set of strings that take a small quantity of information to specific. Word that there are different compression methods we will use; for instance, unbalanced strings like 1112111111112211111111111111111112111 will be lower by at the very least half by creating particular symbols that characterize a number of 1s in sequence. Huffman coding is an instance of an information-theoretically optimum algorithm for creating such transformations.

Lastly, be aware that entropy is context-dependent. The string “the fast brown fox jumped over the lazy canine” might have over 100 bytes of entropy as a easy Huffman-coded sequence of characters, however as a result of we all know English, and since so many 1000’s of data concept articles and papers have already used that actual phrase, the precise entropy is probably round 25 bytes – I’d confer with it as “fox canine phrase” and utilizing Google you may work out what it’s.

So what’s the level of entropy? Basically, entropy is how a lot data it’s a must to memorize. The extra entropy it has, the more durable to memorize it’s. Thus, at first look it appears that you really want passwords which are as low-entropy as attainable, whereas on the similar time being arduous to crack. Nonetheless, as we are going to see beneath this mind-set is slightly harmful.

Power

Now, allow us to get to the subsequent level, password safety towards attackers. The safety of a password is finest measured by the anticipated variety of computational steps that it might take for an attacker to guess your password. For randomly generated passwords, the best algorithm to make use of is brute power: strive all attainable one-character passwords, then all two-character passwords, and so forth. Given an alphabet of n characters and a password of size ok, such an algorithm would crack the password in roughly n^ok time. Therefore, the extra characters you utilize, the higher, and the longer your password is, the higher.

There may be one strategy that tries to elegantly mix these two methods with out being too arduous to memorize: Steve Gibson’s haystack passwords. As Steve Gibson explains:

Which of the next two passwords is stronger, safer, and tougher to crack?

D0g…………………
PrXyc.N(n4k77#L!eVdAfp9

You most likely know it is a trick query, however the reply is: Although the primary password is HUGELY simpler to make use of and extra memorable, it is usually the stronger of the 2! The truth is, since it’s one character longer and comprises uppercase, lowercase, a quantity and particular characters, that first password would take an attacker roughly 95 instances longer to search out by looking out than the second impossible-to-remember-or-type password!

Steve then goes on to jot down: “Nearly everybody has at all times believed or been instructed that passwords derived their power from having “excessive entropy”. However as we see now, when the one obtainable assault is guessing, that long-standing frequent knowledge . . . is . . . not . . . appropriate!” Nonetheless, as seductive as such a loophole is, sadly on this regard he’s useless mistaken. The reason being that it depends on particular properties of assaults which are generally in use, and if it turns into extensively used assaults might simply emerge which are specialised towards it. The truth is, there’s a generalized assault that, given sufficient leaked password samples, can mechanically replace itself to deal with nearly something: Markov chain samplers.

The way in which the algorithm works is as follows. Suppose that the alphabet that you’ve got consists solely of the characters 0 and 1, and you understand from sampling {that a} 0 is adopted by a 1 65% of the time and a 0 35% of the time, and a 1 is adopted by a 0 20% of the time and a 1 80% of the time. To randomly pattern the set, we create a finite state machine containing these chances, and easily run it over and over in a loop.

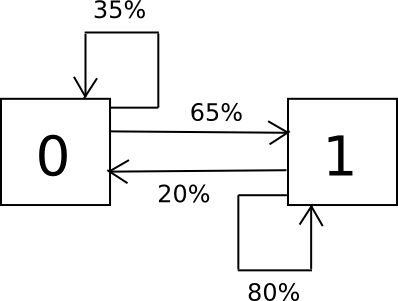
This is the Python code:

import random
i = 0
whereas 1:
    if i == 0:
        i = 0 if random.randrange(100) < 35 else 1
    elif i == 1:
        i = 0 if random.randrange(100) < 20 else 1
    print i

We take the output, break it up into items, and there we have now a approach of producing passwords which have the identical sample as passwords that folks really use. We are able to generalize this previous two characters to a whole alphabet, and we will even have the state preserve observe not simply of the final character however the final two, or three or extra. So if everybody begins making passwords like “D0g…………………”, then after seeing a couple of thousand examples the Markov chain will “study” that folks usually make lengthy strings of durations, and if it spits out a interval it would usually get itself quickly caught in a loop of printing out extra durations for a couple of steps – probabilistically replicating folks’s conduct.

The one half that was overlooked is easy methods to terminate the loop; as given, the code merely offers an infinite string of zeroes and ones. We might introduce a pseudo-symbol into our alphabet to characterize the top of a string, and incorporate the noticed charge of occurrences of that image into our Markov chain chances, however that is not optimum for this use case – as a result of way more passwords are brief than lengthy, it might often output passwords which are very brief, and so it might repeat the brief passwords tens of millions of instances earlier than making an attempt many of the lengthy ones. Thus we’d wish to artificially lower it off at some size, and improve that size over time, though extra superior methods additionally exist like working a simultaneous Markov chain backwards. This basic class of technique is often known as a “language mannequin” – a likelihood distribution over sequences of characters or phrases which will be as easy and tough or as advanced and complex as wanted, and which might then be sampled.

The basic cause why the Gibson technique fails, and why no different technique of that sort can probably work, is that within the definitions of entropy and power there’s an attention-grabbing equivalence: entropy is the logarithm of the variety of prospects, however power is the variety of prospects – in brief, memorizability and attackability are invariably precisely the identical! This is applicable no matter whether or not you’re randomly choosing characters from an alphabet, phrases from a dictionary, characters from a biased alphabet (eg. “1” 80% of the time and “0” 20% of the time, or strings that comply with a specific sample). Thus, it appears that evidently the hunt for a safe and memorizable password is hopeless…

Easing Reminiscence, Hardening Assaults

… or not. Though the essential concept that entropy that must be memorized and the house that an attacker must burn by way of are precisely the identical is mathematically and computationally appropriate, the issue lives in the true world, and in the true world there are a selection of complexities that we will exploit to shift the equation to our benefit.

The primary vital level is that human reminiscence will not be a computer-like retailer of information; the extent to which you’ll precisely keep in mind data usually is determined by the way you memorize it, and in what format you retailer it. For instance, we implicitly memorize kilobytes of data pretty simply within the type of human faces, however even one thing as related within the grand scheme of issues as canine faces are a lot more durable for us. Data within the type of textual content is even more durable – though if we memorize the textual content visually and orally on the similar time it is considerably simpler once more.

Some have tried to benefit from this truth by producing random brainwallets and encoding them in a sequence of phrases; for instance, one may see one thing like:

witch collapse follow feed disgrace open despair creek street once more ice least

A widespread XKCD comedian illustrates the precept, suggesting that customers create passwords by producing 4 random phrases as a substitute of making an attempt to be intelligent with image manipulation. The strategy appears elegant, and maybe taking away of our differing capacity to recollect random symbols and language on this approach, it simply may work. Besides, there’s an issue: it would not.

To cite a latest examine by Richard Shay and others from Carnegie Mellon:

In a 1,476-participant on-line examine, we explored the usability of 3- and 4-word system- assigned passphrases compared to system-assigned passwords composed of 5 to six random characters, and 8-character system-assigned pronounceable passwords. Opposite to expectations, sys- tem-assigned passphrases carried out equally to system-assigned passwords of comparable entropy throughout the usability metrics we ex- amined. Passphrases and passwords had been forgotten at related charges, led to related ranges of person issue and annoyance, and had been each written down by a majority of contributors. Nonetheless, passphrases took considerably longer for contributors to enter, and seem to require error-correction to counteract entry errors. Passphrase usability didn’t appear to extend once we shrunk the dictionary from which phrases had been chosen, diminished the variety of phrases in a passphrase, or allowed customers to vary the order of phrases.

Nonetheless, the paper does depart off on a be aware of hope. It does be aware that there are methods to make passwords which are larger entropy, and thus larger safety, whereas nonetheless being simply as straightforward to memorize; randomly generated however pronounceable strings like “zelactudet” (presumably created through some sort of per-character language mannequin sampling) appear to offer a reasonable acquire over each phrase lists and randomly generated character strings. A probable explanation for that is that pronounceable passwords are prone to be memorized each as a sound and as a sequence of letters, growing redundancy. Thus, we have now at the very least one technique for bettering memorizability with out sacrificing power.

The opposite technique is to assault the issue from the other finish: make it more durable to crack the password with out growing entropy. We can not make the password more durable to crack by including extra mixtures, as that will improve entropy, however what we will do is use what is called a tough key derivation operate. For instance, suppose that if our memorized brainwallet is b, as a substitute of creating the non-public key sha256(b) or sha3(b), we make it F(b, 1000) the place F is outlined as follows:

def F(b, rounds):
    x = b
    i = 0
    whereas i < rounds:
        x = sha3(x + b)
        i += 1
    return x

Basically, we preserve feeding b into the hash operate over and over, and solely after 1000 rounds will we take the output.

Feeding the unique enter again into every spherical will not be strictly crucial, however cryptographers advocate it in an effort to restrict the impact of assaults involving precomputed rainbow tables. Now, checking every particular person password takes a thousand time longer. You, because the official person, will not discover the distinction – it is 20 milliseconds as a substitute of 20 microseconds – however towards attackers you get ten bits of entropy without cost, with out having to memorize something extra. When you go as much as 30000 rounds you get fifteen bits of entropy, however then calculating the password takes near a second; 20 bits takes 20 seconds, and past about 23 it turns into too lengthy to be sensible.

Now, there’s one intelligent approach we will go even additional: outsourceable ultra-expensive KDFs. The concept is to give you a operate which is extraordinarily costly to compute (eg. 2⁴⁰ computational steps), however which will be computed indirectly with out giving the entity computing the operate entry to the output. The cleanest, however most cryptographically difficult, approach of doing that is to have a operate which might by some means be “blinded” so unblind(F(blind(x))) = F(x) and blinding and unblinding requires a one-time randomly generated secret. You then calculate blind(password), and ship the work off to a 3rd celebration, ideally with an ASIC, after which unblind the response once you obtain it.

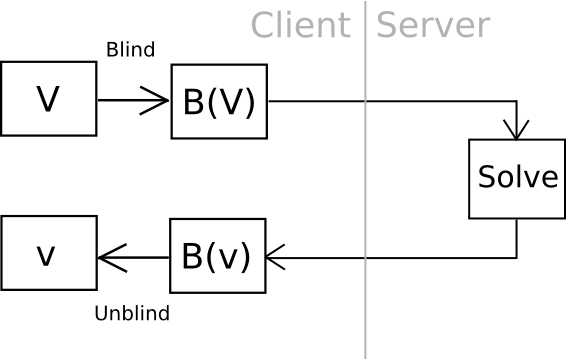
One instance of that is utilizing elliptic curve cryptography: generate a weak curve the place the values are solely 80 bits lengthy as a substitute of 256, and make the arduous drawback a discrete logarithm computation. That’s, we calculate a worth x by taking the hash of a worth, discover the related y on the curve, then we “blind” the (x,y) level by including one other randomly generated level, N (whose related non-public key we all know to be n), after which ship the outcome off to a server to crack. As soon as the server comes up with the non-public key akin to N + (x,y), we subtract n, and we get the non-public key akin to (x,y) – our meant outcome. The server doesn’t study any details about what this worth, and even (x,y), is – theoretically it could possibly be something with the appropriate blinding issue N. Additionally, be aware that the person can immediately confirm the work – merely convert the non-public key you get again into some extent, and ensure that the purpose is definitely (x,y).

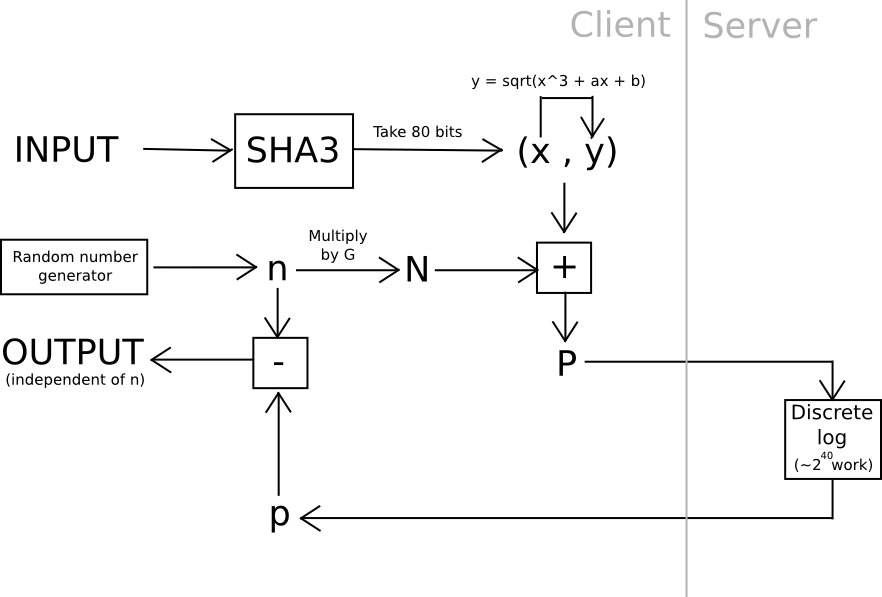
One other strategy depends considerably much less on algebraic options of nonstandard and intentionally weak elliptic curves: use hashes to derive 20 seeds from a password, apply a really arduous proof of labor drawback to every one (eg. calculate f(h) = n the place n is such that sha3(n+h) < 2^216), and mix the values utilizing a reasonably arduous KDF on the finish. Until all 20 servers collude (which will be prevented if the person connects by way of Tor, since it might be inconceivable even for an attacker controlling or seeing the outcomes of 100% of the community to find out which requests are coming from the identical person), the protocol is safe.

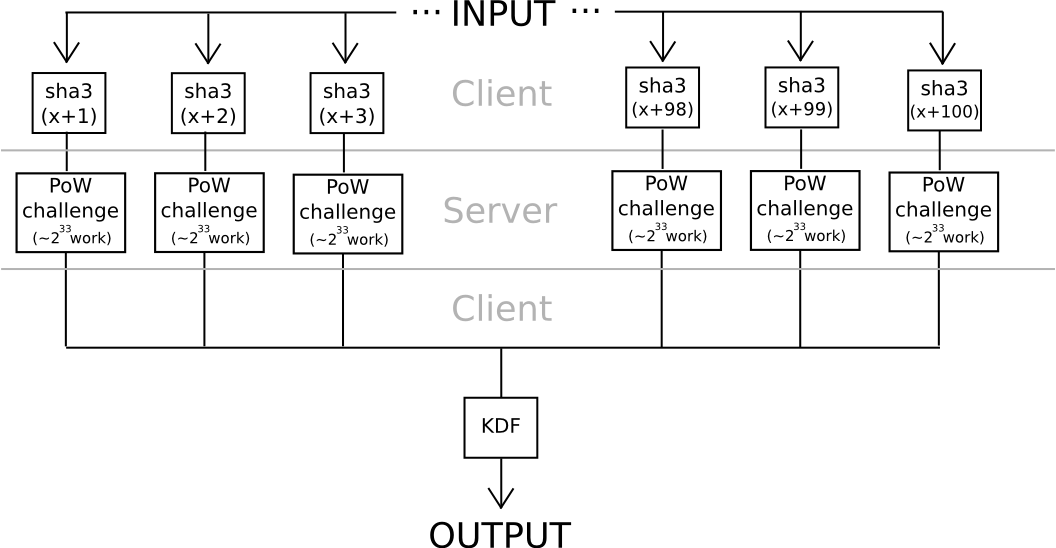
The attention-grabbing factor about each of those protocols is that they’re pretty straightforward to show right into a “helpful proof of labor” consensus algorithm for a blockchain; anybody might submit work for the chain to course of, the chain would carry out the computations, and each elliptic curve discrete logs and hash-based proofs of labor are very straightforward to confirm. The elegant a part of the scheme is that it turns to social use each customers’ bills in computing the work operate, but in addition attackers’ a lot larger bills. If the blockchain sponsored the proof of labor, then it might be optimum for attackers to additionally attempt to crack customers’ passwords by submitting work to the blockchain, wherein case the attackers would contribute to the consensus safety within the course of. However then, in actuality at this degree of safety, the place 2⁴⁰ work is required to compute a single password, brainwallets and different passwords can be so safe that nobody would even hassle attacking them.

Entropy Differentials

Now, we get to our ultimate, and most attention-grabbing, memorization technique. From what we mentioned above, we all know that entropy, the quantity of data in a message, and the complexity of assault are precisely similar – until you make the method intentionally slower with costly KDFs. Nonetheless, there’s one other level about entropy that was talked about in passing, and which is definitely essential: skilled entropy is context-dependent. The title “Mahmoud Ahmadjinejad” might need maybe ten to fifteen bits of entropy to us, however to somebody dwelling in Iran whereas he was president it might need solely 4 bits – within the listing of crucial folks of their lives, he’s fairly seemingly within the prime sixteen. Your mother and father or partner are fully unknown to myself, and so for me their names have maybe twenty bits of entropy, however to you they’ve solely two or three bits.

Why does this occur? Formally, one of the best ways to consider it’s that for every individual the prior experiences of their lives create a sort of compression algorithm, and underneath totally different compression algorithms, or totally different programming languages, the identical string can have a unique Kolmogorov complexity. In Python, ‘111111111111111111’ is simply ‘1’*18, however in Javascript it is Array(19).be a part of(“1”). In a hypothetical model of Python with the variable x preset to ‘111111111111111111’, it is simply x. The final instance, though seemingly contrived, is definitely the one which finest describes a lot of the true world; the human thoughts is a machine with many variables preset by our previous experiences.

This slightly easy perception results in a very elegant technique for password memorizability: attempt to create a password the place the “entropy differential”, the distinction between the entropy to you and the entropy to different folks, is as massive as attainable. One easy technique is to prepend your individual username to the password. If my password had been to be “yui&(4_”, I’d do “vbuterin:yui&(4_” as a substitute. My username might need about ten to fifteen bits of entropy to the remainder of the world, however to me it is nearly a single bit. That is primarily the first cause why usernames exist as an account safety mechanism alongside passwords even in instances the place the idea of customers having “names” will not be strictly crucial.

Now, we will go a bit additional. One frequent piece of recommendation that’s now generally and universally derided as nugatory is to select a password by taking a phrase out of a ebook or tune. The rationale why this concept is seductive is as a result of it appears to cleverly exploit differentials: the phrase might need over 100 bits of entropy, however you solely want to recollect the ebook and the web page and line quantity. The issue is, after all, that everybody else has entry to the books as nicely, and so they can merely do a brute power assault over all books, songs and flicks utilizing that data.

Nonetheless, the recommendation will not be nugatory; actually, if used as solely half of your password, a quote from a ebook, tune or film is a wonderful ingredient. Why? Easy: it creates a differential. Your favourite line out of your favourite tune solely has a couple of bits of entropy to you, however it’s not everybody’s favourite tune, so to the complete world it might need ten or twenty bits of entropy. The optimum technique is thus to select a ebook or tune that you just actually like, however which can also be maximally obscure – push your entropy down, and others’ entropy larger. After which, after all, prepend your username and append some random characters (even perhaps a random pronounceable “phrase” like “zelactudet”), and use a safe KDF.

Conclusion

How a lot entropy do you have to be safe? Proper now, password cracking chips can carry out about 2³⁶ makes an attempt per second, and Bitcoin miners can carry out roughly 2⁴⁰ hashes per second (that is 1 terahash). All the Bitcoin community collectively does 250 petahashes, or about 2⁵⁷ hashes per second. Cryptographers typically take into account 2⁸⁰ to be a suitable minimal degree of safety. To get 80 bits of entropy, you want both about 17 random letters of the alphabet, or 12 random letters, numbers and symbols. Nonetheless, we will shave fairly a bit off the requirement: fifteen bits for a username, fifteen bits for a very good KDF, maybe ten bits for an abbreviation from a passage from a semi-obscure tune or ebook that you just like, after which 40 extra bits of plan previous easy randomness. When you’re not utilizing a very good KDF, then be at liberty to make use of different elements.

It has turn into slightly widespread amongst safety consultants to dismiss passwords as being basically insecure, and argue for password schemes to get replaced outright. A typical argument is that due to Moore’s legislation attackers’ energy will increase by one little bit of entropy each two years, so you’ll have to carry on memorizing increasingly more to stay safe. Nonetheless, this isn’t fairly appropriate. When you use a tough KDF, Moore’s legislation permits you to take away bits from the attacker’s energy simply as shortly because the attacker features energy, and the truth that schemes akin to these described above, except for KDFs (the reasonable variety, not the outsourceable variety), haven’t even been tried suggests that there’s nonetheless some strategy to go. On the entire, passwords thus stay as safe as they’ve ever been, and stay very helpful as one ingredient of a powerful safety coverage – simply not the one ingredient. Reasonable approaches that use a mixture of {hardware} wallets, trusted third events and brainwallets might even be what wins out ultimately.

Supply hyperlink

from Ethereum – My Blog https://ift.tt/rAD6Y0Z
via IFTTT